

 Os primeiros passos no mundo da química
Os primeiros passos no mundo da química
Caderno de Notas
Aulas
1 l
2 l
3 l
4 l
5 l
6 |
7
Aula 1 Matéria e energia
Nota 1
A temperatura de um gás é uma medida da energia cinética Média dos átomos ou moléculas constituintes. Na animação está representado dois gases ideais em solução gasosa, com uma velocidade cerca de dois trilhões de vezes inferior ao real.
l volta para o texto da aula |
Nota 2
Cada substância apresenta um diagrama de fases, mas todos têm o mesmo aspecto. Nele, cada linha representa determinadas condições de temperatura e pressão externa nas quais duas fases coexistem em equilíbrio. As áreas delimitadas por cada linha representam as condições de temperatura e pressão nas quais uma substância existe em um único estado físico.
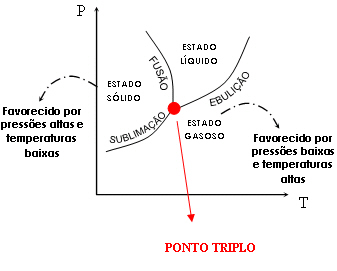
Este diagrama permite entender, por exemplo, por que uma substância é líquida em um lugar e gasosa noutro (as condições de temperatura e pressão podem variar). Além disso, podemos deduzir que a mudança de estado físico pode ocorrer em três situações distintas: à pressão constante e mudando a temperatura (o que fazemos normalmente); à temperatura constante e variando a pressão; ou mudando temperatura e pressão ao mesmo tempo. Veja no gráfico a seguir a primeira situação:
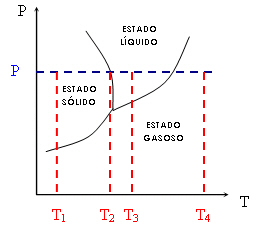
Veja que, para uma mesma pressão P constante (linha azul pontilhada) e variando a temperatura (T1-T4), passamos do estado sólido ao liquido e, finalmente, ao gasoso (T1 < T2 < T3 < T4). Note ainda que T2 representa a temperatura de equilíbrio entre o estado líquido e o estado sólido à pressão P. T2 é, então, a temperatura de fusão. O mesmo ocorreria para o ponto que representa a passagem do estado líquido ao estado gasoso, chamada temperatura de ebulição .
Observe agora este outro gráfico:
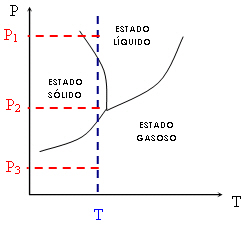
Da mesma forma, você vê que, para uma mesma temperatura T constante (linha azul pontilhada), podemos obter diferentes estados físicos variando apenas a pressão. Observando a figura abaixo, você percebe que, à temperatura constante, o estado gasoso será sempre favorecido por pressões mais baixas, enquanto os estados sólidos e líquidos são favorecidos por pressões mais altas (P1 > P2 > P3).
Através do diagrama de fases podemos entender o motivo pelo qual alguns sólidos sublimam (é o caso, por exemplo, da naftalina e do iodo). Esses sólidos possuem equilíbrio de fases sólido-gás próximo da temperatura e da pressão ambientes. Assim sendo, passam direto do estado sólido ao estado gasoso. Veja o gráfico seguinte:
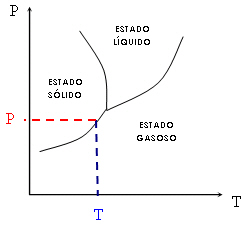
Aula 2 Átomos, Moléculas e Íons
Nota 1
Aqui é importante lembrar que, pra Dalton, a água era HO e não H2O. A fórmula H2O foi estabelecida a partir da interpretação de experimentos de eletrólise da água, quando se observou que a relação dos volumes obtidos dos dois gases era de dois volumes de hidrogênio para um volume de oxigênio. Essa relação foi interpretada de acordo com a hipótese de Avogadro.
volta para o texto da aula | volta para o início
Nota 2
Um exemplo:
Isótopos do Cloro:
17Cl35 (75%) e 17Cl37 (25%)
MACl = (35 . 75) + (37 . 25) / 100 = 35,5 u.m.a
volta para o texto da aula | volta para o início
Nota 3
Um exemplo:
CaF
Ou veja uma lista de diversos sais vendidos comercialmente em: http://www.sigmaaldrich.com/catalog/search/TablePage/16281684
Aula 3 Substâncias simples e compostas e misturas
Nota 1
Substâncias puras são aquelas que apresentam composição fixa e definida, além de propriedades físicas e químicas constantes. As substâncias chamadas de puras são obtidas a partir de processos de separação de misturas homogêneas ou heterogêneas. Tais processos podem ser mecânicos (filtração, decantação) ou baseados nas propriedades físico-químicas das substâncias que compõem as misturas (por exemplo: destilação, recristalização, sublimação). Os processos de purificação de substâncias são usados extensamente nos laboratórios químicos para se obter compostos com alto grau de pureza.
Exemplo de substância pura: a água (H2O) é uma substância que exibe temperatura de fusão (Tfus = 0ºC), temperatura de ebulição (Teb = 100ºC) e densidade (d = 1 g/mL) constantes.
Além disso, as substâncias podem ser classificadas em:
É ainda usual considerar que as substâncias compostas sejam aquelas que podem ser eletroquimicamente decompostas de maneira a fornecer substâncias elementares como produtos. Por exemplo, a água pode ser decomposta em H2 e O2 - duas substâncias elementares. Já o cloreto de sódio pode ser decomposto em sódio metálico e gás cloro (Cl2). Hidróxido de potássio (KOH), um composto ternário, é decomposto por eletrólise em potássio metálico, H2O e O2. Veja as reações de decomposição abaixo:

Sódio metálico.
Fonte: http://www.quiprocura.net/ligacao/liga8.htm

Potássio metálico.
Fonte: http://library.thinkquest.org/C0113863/Potassium.shtml
Em 1807, Sir Humphry Davy, um químico inglês com notável habilidade experimental, passou uma corrente elétrica através de hidróxido de sódio (NaOH, também conhecido por soda cáustica) fundido e observou o aparecimento no catodo de um produto de aparência lustrosa (brilho metálico), sólido à temperatura ambiente. Na verdade, Davy havia produzido sódio (Na) metálico. O mesmo procedimento foi usado para isolar potássio (K) metálico.
No lugar de Davy, como você iria proceder para descobrir se o sólido obtido era uma substância pura ou uma mistura?
Para verificar apenas se o produto consistia numa mistura ou substância pura, você precisaria medir o ponto de fusão do sólido; se o valor da temperatura de fusão permanecesse constante ao longo da fusão completa do material, você poderia afirmar que ele consistia numa substância pura. Os pontos de fusão do sódio e potássio são, respectivamente, 98oC e 63oC. Baixos não!?!
Que experimento você poderia realizar para decidir se o novo sólido isolado consistia numa substância elementar ou numa substância composta?
Nesse caso, você iria precisar passar corrente elétrica através do metal produzido. Como o próprio Davy observou, não há decomposição ao se passar corrente elétrica através do sódio ou potássio metálico, o que mostra que ambas substâncias são elementares (simples).

Cuba usada por Davy em seus experimentos com corrente elétrica.
Fonte: http://www.dkimages.com ...
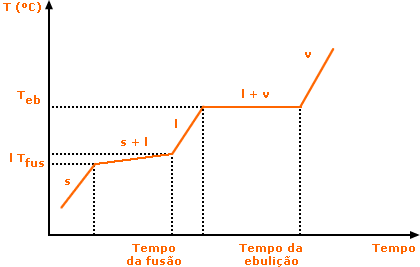
Uma característica principal das substâncias puras é a manutenção da temperatura constante durante uma mudança de estado físico. Ao longo do processo de fusão e ebulição de uma substância pura a temperatura permanece inalterada, o que gera gráficos de temperatura x tempo característicos, como exemplificado abaixo. Lembre-se que durante a mudança de estado físico ocorre um equilíbrio entre as duas fases envolvidas. Você se lembra dos diagramas de fase discutidos na Aula 1?! Se não, reveja a nota 1 da Aula 1
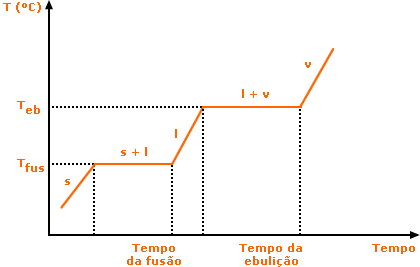
Veja que cada substância apresentará um gráfico distinto, mas todos com o mesmo aspecto. Lembre-se também que a quantidade de substância (ou seja, a sua massa) deslocará apenas o posicionamento do gráfico no eixo do tempo, mas não alterará suas propriedades, isto é, os valores de Tfus e Teb. Pontos de fusão e ebulição são exemplos do que chamamos de propriedades intensivas: são aquelas que não dependem da quantidade de substância. A densidade também é uma propriedade intensiva. A massa e o volume de uma substância são propriedades extensivas. Note que o termo "extensiva" agora define propriedades que dependem da quantidade de matéria. Como regra geral, as substâncias, sejam elas simples ou compostas, só podem ser caracterizadas (ou seja, classificadas e identificadas) por propriedades intensivas. Pense em outros exemplos de propriedades intensivas e extensivas.
Veja que quanto maior for a quantidade de material, mais tempo levará para alcançar as mudanças de estado (linha vermelha do gráfico). Entretanto, tais mudanças continuarão a ocorrer à temperatura de fusão e ebulição constantes.
Misturas apresentam composição variável, mesmo quando conhecidas. Além disso, apresentam propriedades químicas e físicas que variam de acordo com a sua composição, não sendo, portanto, constantes.
As misturas podem ser classificadas em:
Cada porção homogênea de um sistema heterogêneo é chamada de FASE. O sistema água e óleo, por exemplo, é bifásica. Já água, óleo e areia formam um sistema trifásico.
Fique atento, pois a classificação de um sistema em homogêneo ou heterogêneo depende do instrumento ótico a ser utilizado. Assim, a olho nú, o sangue, o leite, a maionese, são misturas homogêneas, mas se olhados ao microscópio serão heterogêneas! Fiquem atentos também à diferença entre sistema (homogêneo e heterogêneo) e mistura!
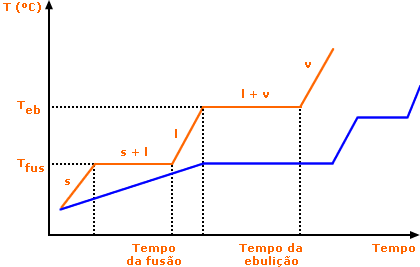
Como apresentam propriedades que dependem diretamente de sua composição, as misturas não apresentam pontos de fusão e ebulição característicos como as substâncias puras, e sim faixas de fusão e ebulição. Dizemos então, que uma mistura funde entre 50 e 55ºC, por exemplo. Desta forma o gráfico de temperatura x tempo para uma mistura comum será diferente do de uma substância pura. Vejamos:
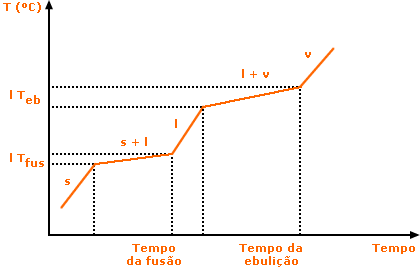
Há dois tipos de misturas muito importantes na Química, chamadas de misturas eutéticas e misturas azeotrópicas. Esses dois tipos de misturas apresentam características particulares como veremos abaixo.
Mistura Eutética - É o tipo de mistura que funde à temperatura constante, mas apresenta uma faixa de ebulição. Um exemplo importante deste tipo de mistura é a solda 63% Sn e 37% Pb.
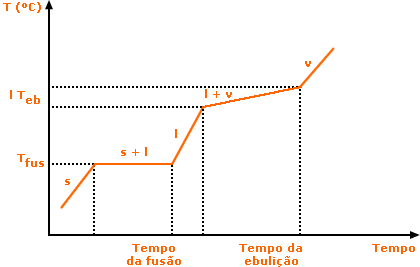
Mistura Azeotrópica - É o tipo de mistura que apresenta uma faixa de temperatura fusão, mas exibe temperatura de ebulição constante. Um exemplo importante deste tipo de mistura é o álcool comum (96°gL).
Aula 4 Mol e massa molecular
Nota 1
| Grandeza | Nome | Plural | Símbolo |
| comprimento | metro | metros | m |
| área | metro quadrado | metros quadrados | m² |
| volume | metro cúbico | metros cúbicos | m³ |
| ângulo plano | radiano | radianos | rad |
| tempo | segundo | segundos | s |
| freqüência | hertz | hertz | Hz |
| velocidade | metro por segundo | metros por segundo | m/s |
| aceleração | metro por segundo por segundo |
metros por segundo por segundo |
m/s² |
| massa | quilograma | quilogramas | kg |
| massa específica | quilograma por metro cúbico |
quilogramas por metro cúbico |
kg/m³ |
| vazão | metro cúbico por segundo |
metros cúbicos por segundo |
m³/s |
| quantidade de matéria | mol | mols | mol |
| força | newton | newtons | N |
| pressão | pascal | pascals | Pa |
| trabalho, energia quantidade de calor |
joule | joules | J |
| potência, fluxo de energia | watt | watts | W |
| corrente elétrica | ampère | ampères | A |
| carga elétrica | coulomb | coulombs | C |
| tensão elétrica | volt | volts | V |
| resistência elétrica | ohm | ohms | Ω |
| condutância | siemens | siemens | S |
| capacitância | farad | farads | F |
| temperatura Celsius | grau Celsius | graus Celsius | °C |
| temp. termodinâmica | kelvin | kelvins | K |
| intensidade luminosa | candela | candelas | cd |
| fluxo luminoso | lúmen | lúmens | lm |
| iluminamento | lux | lux | lx |
Ver na aba Saiba Mais algumas referências sobre o Sistema Internacional de Unidades.
volta para o texto da aula | volta para o início
Nota 2
Como você já estudou, a massa atômica representa a média ponderada dos números de massa dos átomos constituintes e de seus isótopos. Para calcular a massa molecular, basta somar as massas atômicas de todos os elementos presentes na molécula, levando em conta também suas quantidades. Assim:
| H2O | ⇒ | MM = 2 x MAH + MAO MM = (2 x 1) + 16 = 18u |
| Ca(OH)2 | ⇒ | MM = MACa + 2 x (MAH + MAO) MM = 40 + 2 x (1+16) = 74u |
| NaNO3 | ⇒ | MM = MANa + MAN + 3 x MAO MM = 23 + 14 + (3 x 16) = 85u |
Obs. 1: u é o símbolo da massa atômica unificada (ou uma), que é estabelecida como sendo 1/12 da massa do Carbono-12, que é o seu isótopo mais estável. A massa atômica de um dado isótopo do Urânio é 92 u, isto indica que o isótopo possui 92 vezes "mais massa" que 1/12 da massa do Carbono-12.

Obs. 2: 1 mol de um gás ideal (ou perfeito), à temperatura e à pressão padrão (T = 273,15 K e p = 101 325 Pa), ocupa sempre o mesmo volume (aproximadamente 0,0224 m3, ou 22,4L). Ou seja, um balão de 2,2 litros deve conter, aproximadamente, 0,1 mol de qualquer gás (quer seja He, H2, CH4, Cl2 ou qualquer outra molécula que esteja gasosa nestas condições). Este é um método comum de estimar a quantidade de matéria para gases quaisquer, aplicando-se as correções necessárias se os gases não puderem ser considerados perfeitos.
volta para o texto da aula | volta para o início
Nota 3
Estabelecemos agora a primeira relação numérica entre duas grandezas muito importantes em Química: mol e massa.
1 mol __________ massa molar (g)
Lembre que a massa molar tem valor numérico igual à massa atômica para átomos e à massa molecular para moléculas, porém sua unidade será o grama (g). Assim:
| 1 molH2O | 18g |
| 1molFe | 56g |
| 1molNaNO3 | 85g |
volta para o texto da aula | volta para o início
Nota 4
Agora estamos aumentando um pouco mais nossas relações numéricas. Podemos fazer a relação entre mol e a quantidade de partículas. Veja que em um mol sempre haverá 6,02 x 1023 partículas (assim como em 1 dúzia há sempre 12 unidades).
1 mol ______ massa molar (g) _____6,02 x 1023 partículas
Lembre que podemos medir um mol de qualquer coisa; assim, essas partículas poderão ser qualquer coisa. Desta forma:
| 1 molH2O | 18g | 6,02 x 1023 moléculas |
| 1molFe | 56g | 6,02 x 1023 átomos |
| 1molNaNO3 | 85g | 6,02 x 1023 moléculas |
| 1 molbatatas | 6,02 x 1023 batatas (note que não temos massa molar para batatas, mas podemos estimar o peso de um mol de batatas sabendo o peso de uma) |
Veja que 1 mol de ferro, ou 56g de ferro ou 6,02 x 1023 átomos de ferro, representam a mesma quantidade de ferro, expressa em unidades diferentes.
Obs.: Comumente arredondamos a constante de Avogadro para 6,0x1023 por uma facilidade de conta. Mas veja que esse arredondamento é grosseiro, uma vez que estamos diminuindo uma quantidade de 0,02 x 1023 partículas, ou seja, 2.000.000.000.000.000.000.000 de partículas!
volta para o texto da aula | volta para o início
Nota 5
| Moléculas H2SO4 | Átomos H | Átomos S | Átomos O | Átomos totais |
| 1 | 2 | 1 | 4 | 7 |
| 20 | 40 | 20 | 80 | 140 |
| 5893 | 2 x 5893 | 1 x 5893 | 4 x 5983 | 7 x 5983 |
| 6 x 1023 | 2 x 6 x 1023 | 1 x 6 x 1023 | 4 x 6 x 1023 | 7 x 6 x 1023 |
| Mas como 1 mol = 6 x 1023 partículas | ||||
| 1 mol | 2 mol | 1mol | 4mol | 7mol |
Aula 5 Soluções e unidades de concentração
Nota 1
Basta estar de olhos abertos para perceber que o ambiente ao nosso redor é preenchido de matéria com formas e propriedades distintas. A maior parte da matéria que nos deparamos na natureza consiste de misturas. Muitas dessas misturas são homogêneas, ou seja, seus componentes estão de tal maneira misturados no nível atômico e molecular, que a mistura adquire um aspecto macroscópico uniforme, monofásico. As misturas homogêneas são denominadas soluções. É curioso observar a natureza e perceber que, apesar da grande diversidade de substâncias químicas, a maior parte da matéria existente trata de misturas homogêneas. O ar ao nosso redor é uma solução e a água dos oceanos, que preenche 2/3 do espaço da Terra, também é uma solução.
As soluções podem ser gasosas, líquidas ou sólidas. O estado físico de uma determinada solução depende das propriedades físicas das substâncias que a compõe. Cada substância de uma solução é chamada de componente. O componente em maior quantidade (ou maior fração molar) é o SOLVENTE da mistura e os outros componente são chamados de SOLUTOS. Na formação de uma solução, os solventes solubilizam os solutos e estes são solvatados pelo solvente. No caso da água mineral, por exemplo, o solvente é a água e os solutos são os sais minerias dissolvidos. No ar, o gás N2 é o solvente e os outros gases, incluindo o oxigênio (O2), são os solutos. Veja abaixo alguns exemplos de soluções.
| Estado da solução | Estado do solvente | Estado do soluto | Exemplo |
| gás | gás | gás | ar |
| líquido | líquido | gás | oxigênio dissolvido na água, água gasosa, ácido muriático |
| líquido | líquido | líquido | álcool na água, água oxigenada |
| líquido | líquido | sólido | água mineral, gatorade® |
| sólido | sólido | gás | hidrogênio difundido em paládio |
| sólido | sólido | líquido | mercúrio na prata, amálgamas em geral |
| sólido | sólido | sólido | bronze, aço, ligas metálicas em geral, sal iodado, comprimidos de medicamento |
As soluções sólidas metálicas (ligas metálicas) ocupam um lugar de destaque no mundo contemporâneo. Veja alguns exemplos:
| Liga metálica | Componentes | Característica | Uso |
| Latão | Cobre e zinco | Resistente à corrosão | Navios, tubos |
| Bronze | Cobre e estanho | Resistente à corrosão | Moedas, sinos |
| Aço | Ferro e carbono | Resistente à corrosão | Navios, utensílios domésticos |
| Aço inoxidável | Aço e cromo | Resistente à corrosão | Talheres, utensílios domésticos |
| Aço-Níquel | Aço e níquel | Resistência mecânica | Canhões, material de blindagem |
| Aço-Tungstênio | Aço e tungstênio | Alta dureza | Brocas, pontas de caneta |
| Alnico | Aço, alumínio, níquel e cobalto | Propriedades magnéticas | Fabricação de ímãs |
| Amálgama | Mercúrio, prata e estanho | Alta resistência e dureza | Restauração de dentes |
| Ouro 18 quilates | Ouro e cobre | Alta ductibilidade e maleabilidade | Jóias |
| Prata de lei | Prata e cobre | Aumento da dureza | Utensílios domésticos, ornamentos |
Uma solução é formada quando uma substância (soluto) se dispersa uniformemente em outra (solvente). Excetuando-se as misturas gasosas, todas as outras envolvem substâncias em fase condensada, líquida ou sólida. Para que haja a formação da solução, o soluto precisa se dissolver completamente no solvente. Em outras palavras, a substância em menor quantidade precisa ser solúvel no solvente, porque se não for, a mistura não adquire um aspecto homogêneo.
O processo de dissolução, ou solubilização, de um soluto é governado pelas forças de interação solvente-solvente, soluto-soluto e soluto-solvente. Essas forças são definidas pelos tipos de interações intermoleculares existentes nas substâncias interagentes.
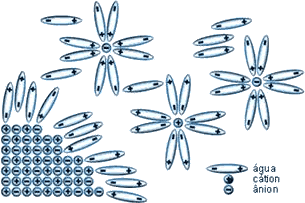
As soluções aquosas de substâncias iônicas têm importância única na Química e no nosso dia-a-dia, como pôde ser lido no próprio texto da aula. No caso dos sais inorgânicos, as forças de atração e repulsão entre os íons e seu arranjo geométrico são responsáveis por suas propriedades, bem como por seus altos pontos de fusão. Quando são fundidos, ocorre o afastamento entre os íons, as forças de interação são enfraquecidas e o retículo cristalino é destruído, permitindo a movimentação dos íons, de forma que, sob ação de um campo elétrico, eles se orientam e se movimentam de modo a estabelecer condutividade iônica por meio do material fundido.
Os cristais iônicos oferecem resistência considerável ao rompimento do retículo, mas são solúveis em água. A solubilidade em água pode ser justificada pelo fato de a molécula de água ser um dipolo elétrico (apresentar alta constante dielétrica), que, por atração eletrostática, separa os íons e destrói a rede cristalina. Assim, a água se caracteriza como um ótimo solvente para as substâncias iônicas. Leia um pouco mais sobre esse tema num excelente artigo publicado em 2004 em Química Nova, uma revista da Sociedade Brasileira de Química. Leia também sobre a diferença entre solubilização (ou dissolução) e solvatação.
volta para o texto da aula | volta para o início
Nota 2
Formação de soluções aquosas eletrolíticas a partir da solublização de compostos, iônicos (sais) ou moleculares polares, completamente dissociáveis em água:
HCl(g) → H+(aq) + Cl-(aq)
KCl(s) → K+(aq) + Cl-(aq)
KIO3(s) → K+(aq) + IO3-(aq)
CaCl2(s) → Ca2+(aq) + 2 Cl-(aq)
Na2SO4(s) → 2 Na+(aq) + SO42-(aq)
NaHCO3(s) → Na+(aq) + HCO3-(aq)
KOH(s) → K+(aq) + OH-(aq)
H2SO4(l) → H+(aq) + HSO4-(aq)
Nas reações de dissociação eletrolítica acima, os índices subescritos, (g), (l) e (s), informam os estados físicos da substância: gasoso, líquido e sólido, respectivamente. O índice (aq) indica que a espécie iônica está solvatada pela água (espécie hidratada).
Os íons formados em solução são chamados de eletrólitos. As substâncias eletrolíticas são aquelas que produzem eletrólitos quando solubilizadas em água. Essas substâncias podem ser iônicas (por exemplo: os sais NaCl, NaNO3, CuSO4 etc.), moleculares polares completamente dissociáveis em água (por exemplo: os ácidos HCl, H2SO4, HNO3 etc.) ou não (por exemplo: NH3, CH3COOH, H2S, etc.) e até mesmo apolares (por exemplo: CO2). Nestes dois últimos casos, os eletrólitos são produzidos por hidrólise e não apenas por simples dissociação:
NH3(g) + H2O → NH4+(aq) + OH-(aq)
CO2(g) + H2O → H+(aq) + HCO3-(aq)
HCO3-(aq) + H2O → H3O+(aq) + CO32-(aq)
Em virtude da formação de íons hidratados em solução, as soluções eletrolíticas conduzem corrente elétrica moderadamente. Clique aqui para ler mais sobre condutividade iônica. Leia também um texto interessante sobre a teoria de dissociação eletrolítica de Arrhenius.
Valores típicos de condutividade elétrica em S/m (Siemens/metro):
| Condutores iônicos | Cristais iônicos | < 10-16-10-2 |
| Eletrólitos sólidos | 10-1-103 | |
| Eletrólitos fortes (soluções aquosas) |
10-1-103 | |
| Condutores Eletrônicos | Metais | 103-107 |
| Semicondutores | 10-7-105 | |
| Isolantes | < 10-10 |
Como a concentração molar da substância eletrolítica determina a concentração dos eletrólitos em solução?
Considere, por exemplo, uma solução aquosa de HCl. Nela, não há em solução moléculas intactas de HCl, apenas os íons H+ e Cl-, oriundos da dissociação completa da substância cloreto de hidrogênio, que é gasosa à temperatura ambiente. Assim, por causa da relação molar H:Cl (igual a 1:1), que pode ser observada pela reação de dissociação eletrolítica, a concentração de íons H+ é idêntica a de íons Cl-. Por exemplo, dizer que a concentração de uma solução de HCl é igual a 10 mol/L significa dizer dizer que a concentração do íon H+ é 10 mol/L assim como é 10 mol/L a concentração de cloreto. Na formação de uma solução de KCl acontece a mesma coisa. Uma concentração de KCl igual a 0,1 mol/L informa que a concentração dos elétrólitos K+ e Cl- também é 0,1 mol/L. Esse tipo de relação só pode ser estabelecida ente concentração molares, já que nestas a razão molar também é preservada. No caso do sulfato de sódio (Na2SO4), dizer que a concentrção do sal é 1,0 mol/L, por exemplo, significa dizer que a concentração do íon Na+ é duas vezes maior que essa, igual a 2,0 mol/L, e a concentração do íon sulfato é 1,0 mol/L, respeitando as proporções molares estabelecida na reação de dissociação.
volta para o texto da aula | volta para o início
Nota 3
Concentrem-se em alguns probleminhas de cálculo de concentração de soluções! A técnica usada para a resolução dos problemas envolve análise dimensional.
Problema 1
Calcule a massa, em g, de 25 mL de um líquido de densidade d = 1,80 g/mL.
Solução:
Como d = m/v ou m = d.v;
m = 1,80 g/mL x 25 mL = 45 g (cancelam-se mL-1 e mL).
Problema 2
Quantos mililitros de H2SO4 a 20% são necessários para preparar 200 mL de uma solução 0,30 mol/L de H2SO4?
Esta é uma situação típica de surgir no laboratório, e a análise dimensional vai simplificar a operação e reduzir o tempo gasto nos cálculos. Deve-se notar que a concentração percentual é em geral aqui como massa de soluto por volume (100 mL) da solução.
Solução:
Vejamos, por partes, como se resolve o problema, iniciando pela solução que se quer obter no final.
Uma solução 0,30 mol/L tem, por definição, 0,3 moles de soluto em 1000 mL de solução. Logo, se queremos 200 mL, teremos:
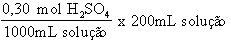
Em seguida, vamos ver quantos gramas de H2SO4 estão presentes em 200 mL de solução:
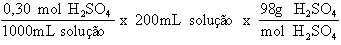
Como a solução estoque de H2SO4, a partir da qual será feita a nova solução 0,30 mol/L, tem a concentração de 20%, chegamos ao final do cálculo:
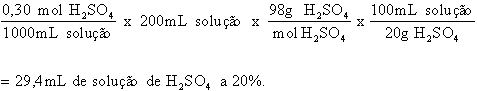
Problema 3
O peridrol é uma água oxigenada a 40 %p/v. Qual é a sua concentração expressa em volumes de O2?
Solução:
Por definição, volume de O2 = volume de O2(g), em mL, liberado por 1 mL de solução de H2O2. A equação da reação é:
H2O2(aq) → H2O(l) + ½ O2(g)
Logo,
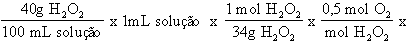
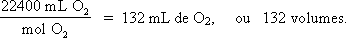
Problema 4
Qual é a concentração em %p/v da água oxigenada a 20 volumes?
Solução:
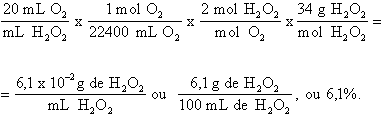
A concentração de um determinado soluto numa solução pode ser dada qualitativa ou quantitativamente. Do ponto de vista qualitativo, os termos "diluída" e "concentrada" são usados para descrever, respectivamente, uma solução com concentração de soluto relativamente baixa e uma solução com concentração de soluto alta. Os termos "alto teor" e "baixo teor" também são cotidianamente usados para descrever qualitativamente as concentrações de solutos. Quem nunca ouviu falar que o teor de álcool etílico de uma bebida alcoólica é baixo ou alto, ou ainda que o teor de gases poluentes na atmosfera é alto numa cidade industrial? Esses termos já estão em domínio público e nos fornecem uma dimensão da quantidade relativa de um determinado soluto numa solução. É claro que para se usar esses termos qualitativos é necessrio ter uma referência que nos diz a partir de quanto se deve usar diluída ou concentrada, ou quando se deve usar alto e baixo teor.
Para evitar confusões na caracterização de uma solução, é necessário estabelecer quantitativamente a concentração dos solutos. Esse valor numérico de concentração tem de estar atrelado a uma unidade de concentração e pode ser calculado ou medido experimentalmente a partir de técnicas específicas para esse fim. As técnicas mais usadas em laboratório para se determinar a concentração de um soluto são: espectroscopia eletrônica (UV-vis), cromatografia líquida e gasosa e espectrometria por absorção atômica.
Diversas são as unidades de concentração. Todas elas são unidades derivadas e podem, a partir de sua definição, ser convertidas em outras unidades. As unidades mais comuns em Química são: fração molar; porcentagem peso-peso (% p/p), porcentagem peso-volume (% p/v) e porcentagem volume-volume (% v/v); g/L e submúltiplas (mg/L, µg/L etc); ppm e ppb; molaridade (mol/L); molalidade (mol/kg).
A molalidade é definida por:
molalidade (mol/kg) = m (g) do soluto / kg de solvente.
Aqui uma novidade: no cálculo da molalidade, no denominador não é mais quantidade de solução e, sim, massa (em kg) de solvente apenas. Curioso, não!
Um resumo das unidades de concentração de maior interesse à Química pode ser encontrado nos endereços abaixo:
volta para o texto da aula | volta para o início
Nota 4
C (g/L) = m (g) / Vt (L) e M (mol/L) = n (mol) / Vt (L)
A massa de um mol de qualquer espécie química tem o valor numérico, em gramas, de sua massa expressa em u.m.a.; portanto, para achar o número de mols de uma determinada substância a partir de sua massa (em gramas), basta dividir essa massa pela massa molar (MM, em gramas/mol) da substância. Assim:
n (mol) = m (g) / MM (g/mol)
Agora, substituindo o valor de n na expressão da molaridade e rearrumando os termos, temos:
M (mol/L) = m / (MM x Vt) ou C (g/L) = M (mol/L) x MM (g/mol)
Você pode chegar à mesma conclusão apenas rearranjando as unidades das grandezas físicas em questão. Assim você estará realizando uma análise dimensional!
volta para o texto da aula | volta para o início
Nota 5
C (g/L) = m (g) / Vt (L) e d (g/mL) = mt (g) / Vt (mL) (aqui é a densidade da solução e não de uma substância pura)
%p/p = [m (g) / 100 g (de solução)] x 100
Nas expressões acima, sempre está sendo considerado o volume total de solução (Vt), expresso em unidades de volume diferentes, a saber: litro (L) e mililitro (mL). Para estabelecer uma relação entre C e %p/p, é necessária uma conversão nas unidades de volume. Como 1 L = 1000 mL:
mt / d (g/mL) = [m (g) / C (g/L)] x 1000
Rearrumando a expressão em função de C:
C = (m / mt) x 1000 x d
Mas como: %p/p = (m / mt) . 100 , temos:
C = 10 x d x %p/p
Desse modo, pode-se dizer que:
C = M x MM = 10 x d x %p/p
OBS.: Fique atento, pois densidade (d) NÃO é uma unidade de concentração. Lembre que toda unidade de concentração mede a relação entre a quantidade de soluto e a quantidade de solução. Já a densidade (d = mt / Vt) considera a massa total (mt) da solução (soluto + solvente) e também o volume total (Vt) da mesma.
Aula 6 Reações químicas
Nota 1
Considerações teóricas: Toda reação química é um rearranjo de átomos e moléculas.
Em toda transformação química ocorre uma reação química que pode ser representada por uma equação química balanceada ou ajustada.
Em uma equação química, antes da seta são representados os reagentes e, após a seta, os produtos.
Podemos dizer, filosoficamente, que uma reação química encerra em si a mutação e a permanência simultaneamente, pois, como disse Lavoisier, “nenhuma nova criação ou destruição da matéria está dentro do alcance da atividade química”.
Dessa maneira, em uma reação química a massa se conserva porque os átomos não são destruídos e, portanto, a equação que a representa deve ser balanceada.
Balancear uma equação química é encontrar os coeficientes das substâncias que tornam o número total de átomos de cada elemento igual nos reagentes e nos produtos.
Os coeficientes são os menores números inteiros que ajustam a equação e representam a proporção em número de mols entre os participantes da reação.
Vamos representar a síntese do Aℓ2Br6:
Aℓ(s) + Br2 (l) --> Aℓ2Br6(s) não balanceada
Para ajustá-la, devemos igualar o número de átomos de cada elemento antes e depois da seta.
| Aℓ reag | Br reag | Aℓ prod | Br prod |
| 1 | 2 | 2 | 6 |
Basta multiplicar o Aℓ reagente por 2 e o Br regente por 3.
2 Aℓ(s) + 3 Br2 (l) --> Aℓ2Br6(s) equação balanceada
Nota: Os índices s, l e g significam sólido, líquido e gasoso, respectivamente, e indicam o estado físico de cada substância. Há ainda a notação aq, que significa em água ou aquoso.
Reações de síntese são aquelas em que dois ou mais reagentes dão origem a um e somente um produto. Uma síntese muito importante é a síntese da amônia.
N2(g) + H2(g) --> NH3(g) não balanceada
| N reag | H reag | N prod | H prod |
| 2 | 2 | 1 | 3 |
Como entre 2 e 3 o mínimo múltiplo comum é 6, devemos multiplicar o H reagente por 3 e o H produto por 2; conseqüentemente estaremos multiplicando também o N produto por 2, pois os coeficientes só podem ser introduzidos antes das fórmulas.
N2(g) + 3 H2(g) --> 2 NH3(g) equação balanceada
Reações de decomposição são aquelas na qual um e somente um reagente se decompõe formando duas ou mais substâncias.
A decomposição térmica do carbonato de cálcio é um exemplo de reação de decomposição e pode ser representada pela seguinte equação já ajustada:
CaCO3(s) --> CaO(s) + CO2(g)
Outra decomposição importante é a da água oxigenada que ocorre por ação da luz.
2 H2O2(aq) --> 2 H2O(l) + O2(g)
Reações em solução aquosa: quando misturamos duas substâncias, poderá ou não ocorrer reação entre elas. Quatro tipos importantes de processos provocam a ocorrência de reações quando os reagentes se misturam em solução aquosa.
a) Precipitação - forma-se um produto insolúvel, o precipitado.
Pb(NO3)2(aq) + 2 KI(aq) --> PbI2(s) + 2 KNO3(aq)
O produto insolúvel PbI2 é indicado pelo estado físico sólido.
b) Reações ácido-base - nessas reações o íon H+ e OH- se combinam para formar água.
HNO3(aq) + KOH(aq) --> KNO3(aq) + H2O(l)
As reações entre ácidos e bases fortes são denominadas reações de neutralização, pois, uma vez completada a reação, a solução restante é neutra.
Nota: Não devemos esquecer que a amônia é uma base e reage com a água formando o íon amônio e o íon hidroxila:
NH3(g) + H2O(l) --> NH4(aq)+ + OH(aq)-
A reação da amônia com o HNO3 também é um exemplo de reação ácido-base, em que os íons H+ do HNO3 se combinam com os íons OH- produzidos pela reação da amônia.
NH3(g) + HNO3(aq) --> NH4 NO3(aq)
c) Reações com desprendimento de gás – forma-se um produto que nas condições ambientes é um gás. Destacam se as reações com carbonatos que formam ácido carbônico (H2CO3), que se decompõe em gás carbônico (CO2) e água (H2O).
NiCO3(s) + 2 HNO3(aq) --> Ni NO3(aq) + H2CO3(aq)
Como: H2CO3(aq) --> CO2(g) + H2O(l), podemos escrever
NiCO3(s) + 2 HNO3(aq) --> Ni (NO3)2(aq) + CO2(g) + H2O(l)
d) Reações de oxi-redução – neste caso, o processo é a transferência de elétrons de uma substância parta outra.
Cu(s)0 + 2 Ag+NO3-(aq) --> Cu2+(NO3)2-(aq) + 2Ag(s)0
Neste caso o cobre (Cu) perdeu dois elétrons para a prata (Ag), sendo 1 elétron para cada átomo de prata. Nessa reação, os elétrons foram transferidos do cobre para a prata. Dizemos que a prata sofreu redução e o cobre sofreu oxidação.
volta para o texto da aula | volta para o início
Nota 2
A energia de uma reação varia ao longo da conversão de reagentes a produtos. Para uma reação exotérmica, temos o seguinte perfil de variação de energia:
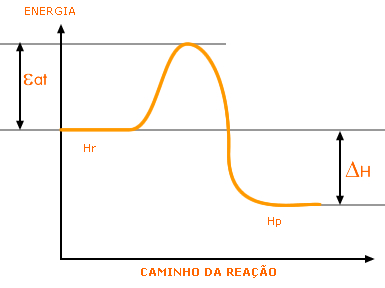
Nesta reação, a entalpia dos produtos (Hp) é menor do que a dos reagentes (Hr), então ocorre liberação de calor (DH < 0). Entretanto, a passagem de reagentes para produtos não é direta: existe um estado de transição, que corresponde ao instante de quebra das ligações químicas nos reagentes e formação das novas ligações existentes nos produtos, que é de maior energia que os reagentes. Assim, é necessário que se forneça a energia necessária para que seja atingido o estado de transição (energia de ativação, Ea) para que uma reação ocorra, mesmo ela sendo exotérmica. Os catalisadores atuam nas reações diminuindo a energia de ativação, por estabilizarem os estados de transição, fazendo com que seja necessário o fornecimento de uma menor qunatidade de energia para que a reação ocorra.
Aula 7 Quantificando as Reações: Noções de Estequiometria
Nota 1
Estequiometria é a parte da Química em que são investigadas as proporções dos elementos que se combinam em um composto ou dos compostos que reagem numa reação. Divide-se em estequiometria de fórmulas e estequiometria de reações. Decorre das leis ponderais de Lavoisier e Proust, isto é da Lei da Conservação da Massa e da Lei das Proporções Fixas e Definidas. Através do cálculo estequiométrico é possível prever a quantidade de produto que será obtida em uma reação química.
A) Vamos começar nosso estudo por uma reação bem simples: a síntese da amônia. A equação química que representa o fenômeno é
N2(g) + 3 H2(g) → 2 NH3(g)
De acordo com nossos conhecimentos sobre as fórmulas, podemos ler a equação acima da seguinte forma:
1 molécula de N2 reage com 3 moléculas de H2 para formar 2 moléculas de NH3.
Essa é uma leitura que se aplica ao mundo microscópico. Sabemos, quase intuitivamente, que se tivermos 10 moléculas de N2 serão necessárias 30 moléculas de H2 e se formarão, no máximo, 20 moléculas de NH3. Agora, se tivermos um conjunto de 6,02 ×1023 moléculas de N2, serão necessárias (3 x 6,02 ×1023) moléculas de H2 e se formarão, no máximo, (2 x 6,02 ×1023 ) moléculas de NH3. O número de moléculas pode ser qualquer um, desde que a proporção se mantenha 1: 3: 2. Mas lembre-se de que um conjunto de 6,02 ×1023 elementos corresponde a 1 mol; assim:
1 mol de N2 reage com 3 mol de H2 para formar 2 mol de NH3.
Essa proporção, feita EM MOL, é o que chamamos de proporção estequiométrica. Repare que os números que determinam essa proporção são exatamente os números que balanceiam a equação. Esses números são, então, chamados de coeficientes estequiométricos.
Mas no mundo macroscópico não nos adianta relacionar moléculas; necessitamos de grandezas mais eficientes no cotidiano, como massa e volume. A partir da proporção em número de mol é possível expressar a relação em massa entre reagentes e produtos e, quando for interessante, a relação em volumes. Lembre que:
1 mol −−−− massa molar (g) −−−− 6,02 x 1023 partículas −−−− 22,4L (nas CNTP)
Dessa forma, podemos fazer a mesma leitura em massa, sabendo a massa molar de cada participante da reação.
Temos N2 = 28 g/mol, H2 = 2 g/mol, NH3 = 17 g/mol; obteríamos, assim:
(1 mol × 28g/mol) de N2 reage com (3 mol × 2 g/mol de H2) para formar (2 mol × 17g/mol de NH3), o que equivale a:
28g de N2 reage com 6g de H2 para formar 34g de NH3.
Atenção: Não confunda a proporção em número de mols com a proporção em massa. Esta última pode ser obtida da leitura acima, e seria, nos menores números, 14g de N2 reage com 3g de H2 para formar 17g de NH3. Além disso, podemos comprovar a Lei da Conservação da Massa. Note que teremos 34g de reagentes (28g + 6g) e formaremos 34g de produto (a massa inicial dos reagentes é igual à massa final dos produtos).
Assim, se colocarmos, por exemplo, 35g de N2 e 6g de H2, continuaremos formando 34g de NH3 (7g de N2 estarão em excesso). Não adianta aumentar a quantidade de apenas um reagente, o aumento deve ser de todos e dentro da proporção estequiométrica.
Como nessa reação os reagentes e produtos estão no estado gasoso, supondo esses gases na temperatura de 0° C e pressão de 1 atm, o que significa condições normais de temperatura e pressão (CNTP), ainda poderíamos expressar a síntese da amônia pela relação entre os volumes de reagentes e produtos. Sabemos que, nessas condições, 1 mol de qualquer gás ocupa 22,4L; como sabemos o número de mol de cada participante na reação, podemos escrever:
(1 mol × 22,4L/mol) de N2 reage com (3 mol × 22,4 L/mol) de N2 para formar (2 mol × 22,4L/mol de NH3), o que equivale a:
22,4L de N2 reage com 67,6L de H2 para formar 44,8L de NH3.
B) Vejamos um outro exemplo. A equação global a seguir refere-se à transformação que ocorre no alto-forno para a produção de ferro-gusa em uma siderúrgica:
2 Fe2O3(s) + 6 C(s) + 3 O2(g) à 4 Fe(s) + 6 CO2(g)
Considerando a equação acima, o que aconteceria com a quantidade de ferro gusa produzida, se duplicássemos a quantidade de todos os reagentes?
Você deve ter pensado: duplicaria. Oh! E está certo!
Mas se duplicarmos apenas o número de mols do Fe2O3, o que ocorrerá com a quantidade de matéria em mols de ferro-gusa produzida?
Se você respondeu que seria produzida a mesma quantidade, você acertou!
Da equação temos que 2 mol de Fe2O3 produzem 4 mol de Fe; porém, se os demais reagentes não forem também duplicados, 4 mol de Fe2O3 continuarão produzindo 4 mol de Fe, pois a proporção da reação é mantida para qualquer quantidade de reagente (o produto só pode ser obtido mediante todos os reagentes).
Podemos fazer previsões sobre a quantidade de ferro que será obtida a partir de 320kg de óxido férrico, considerando que os demais reagentes estejam em quantidades suficientes ou adequadas. Essa quantidade poderá ser expressa em massa ou em mols de ferro produzido.
- Vamos determinar primeiramente a massa de ferro que será obtida:
Da equação temos que 2 mol de Fe2O3 produzem 4 mol de Fe. A massa molar do Fe2O3 é 160g/mol, e a do Fe é 56g/mol. Como nosso problema é determinar a massa de Fe a partir da massa de Fe2O3, vamos escrever a relação acima em massa:
| Se (2 mol × 160g/mol) de Fe2O3 | produzem | (4 mol x 56g/mol) de Fe, |
| quando tivermos | ||
| 320kg de Fe2O3 | produziremos | X g de Fe ? |
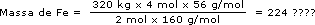
Mas qual será a unidade? Ao cancelarmos as unidades, só restará o kg; portanto, nossa resposta está em kg.
- Agora vamos determinar a quantidade de matéria em mols de Fe que seria obtida com 320kg de Fe2O3.
Da equação temos que 2 mol de Fe2O3 produzem 4 mol de Fe. A massa molar do Fe2O3 é 160 g/mol e a do Fe é 56 g/mol. Como o nosso problema é determinar o número de mols de Fe a partir da massa de Fe2O3, vamos escrever a relação acima em número de mols para o ferro e em massa para o Fe2O3, de acordo com o que foi dado e o que é pedido:
| Se (2 mol × 160g/mol) de Fe2O3 | produzem | 4 mol de Fe |
| quando tivermos | ||
| 320kg de Fe2O3 | produziremos | x mol de Fe ? |
Número de mol de
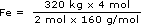
Para cancelar as unidades, é necessário escrever 320kg em g, uma vez que a massa molar é definida como g/mol.
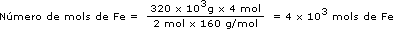
O resultado está de acordo com a primeira determinação, pois 4 × 103 mol de Fe é igual a (4 × 103 mol × 56 g/mol) = 224 × 103g ou 224kg.
- Vamos ainda nesse processo determinar o volume de CO2 que seria obtido nas CNTP com 320kg de Fe2O3. Da equação temos que 2 mol de Fe2O3 produzem 6 mol de CO2.
A massa molar do Fe2O3 é 160g/mol, e o volume molar do CO2 nas CNTP é de 22,4L/mol. Como nosso problema é determinar o volume de CO2 a partir da massa de Fe2O3, vamos escrever a relação acima em massa para o Fe2O3 e em volume para o CO2, de acordo com o que foi dado e o que é pedido:
| Se (2 mol × 160g/mol) de Fe2O3 | produzem | 6 mol × 22,4L/mol de CO2 |
| quando tivermos | ||
| 320kg de Fe2O3 | produziremos | volume de CO2 |
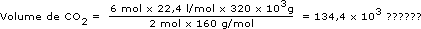
Cancelando as unidades, encontramos nossa resposta em litros, como é coerente com a grandeza volume. O volume de CO2 obtido a partir de 320kg de Fe2O3 com os demais reagentes em quantidades suficientes será de 134,4×103 L.
ATENÇÃO!! Os mesmos resultados anteriores poderiam ter sido obtidos transformando-se todas as unidades para mol e, após, utilizando as relações numéricas, determinarmos a unidade que desejamos. Esse procedimento é o que chamamos de Análise Dimensional. Por ela os itens anteriores são resolvidos de forma muito simples, com ênfase nas unidades. Vejamos...
Em primeiro lugar calcula-se o número de mols de Fe2O3 em 320 kg, isto é, 320x103g:
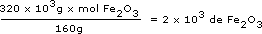
Como o número de mols de Fe é o dobro do número de mols de Fe2O3, temos 4×103 mol de Fe, o que corresponderá em massa a:
Massa de ferro = número de mols de Fe × massa molar do ferro
Massa de ferro = 4 × 103 mol de Fe × 56g/mol = 224 × 103 g de Fe
Como o número de mols de CO2 é o triplo do número de mols de Fe203, o que corresponderá em volume a:
Volume de CO2 = 3 × número de mols de Fe2O3 x volume molar nas CNTP
Volume de CO2 = 6 × 103 mols de CO2 × 22,4L/mol = 134,4 x103 L