Guia de disciplina
Professor responsável: André Luiz Cordeiro dos Santos.
Tutor: Alex Farah Pereira
e-mail do professor: andre.cederj@gmail.com
Endereço de correspondência (para envio de DOCUMENTOS)
Fundação CECIERJ
Diretoria de Extensão
Curso de Extensão em Matemática
Rua da Ajuda, 5 - 16º. andar
Centro - Rio de Janeiro - RJ
CEP 20040-000
I - O CURSO DE EXTENSÃO EM MATEMÁTICA
O Curso de Extensão em Matemática é oferecido em disciplinas com carga horária de 30 horas cada uma. Ao término de cada disciplina em que obtenha aprovação, você receberá uma declaração de conclusão da disciplina, que será enviada ao pólo escolhido no ato da inscrição.
Sendo graduado e aprovado em quatro disciplinas (120h) no período de até seis trimestres letivos consecutivos, você receberá o Certificado de Atualização em Matemática. No caso de licenciando, veja o edital.
Para receber qualquer declaração ou certificado, é necessário que você envie até 05/07, para o endereço de correspondência, os documentos que comprovam o que você declarou na ficha de inscrição: cópia do CPF; cópia da Carteira de Identidade; cópia do diploma que comprove a conclusão do curso de graduação na área específica do curso ou em áreas afins, ou, no caso de licenciandos, declaração oficial da instituição informando que o aluno está cursando o último ano de Licenciatura; se estiver em exercício de magistério, comprovante emitido pela escola pública ou privada.
II - A DISCIPLINA ANÁLISE COMBINATÓRIA
Sabemos que você, professor, não dispõe de tempo e de condições favoráveis para se deslocar do seu local de moradia e/ou trabalho até alguma instituição que esteja ministrando cursos de atualização. Por isso estamos lhe oferecendo esta modalidade de estudar. Seu sucesso dependerá da sua organização individual, mas você não está sozinho nessa tarefa.
Neste guia você terá as informações de que necessita e, em caso de dúvidas, entre em contato com a professor responsável pela disciplina.
Consulte o Cronograma da disciplina, lá você encontrará um resumo das principais datas do curso.
A plataforma é o seu contato virtual e direto com a Fundação e seus professores. Visite-a, pelo menos, quatro vezes por semana. Muitas atualizações e informações importantes serão hospedadas neste ambiente.
Utilize a Sala de Tutoria para postar as dúvidas relacionadas à disciplina que serão respondidas pelo tutor ou pela professor responsável pela disciplina.
Consulte-a regularmente, pois sua dúvida pode já ter sido respondida a um colega seu. Faça perguntas novas, não acumule dúvidas.
No título de sua dúvida, escreva um exemplo ou um exercício de cada vez, por exemplo: "Aula 2 – exemplo 3" ou "Aula 7 – página 68". Desse modo, você facilita a busca que um colega faria e evita que a mesma pergunta seja feita várias vezes.
Para usar o editor matemático na Sala de Tutoria, clique no símbolo 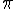 .
.
Não utilize a Sala de Tutoria para esclarecimentos sobre notas e correção de avaliações; por se tratar de assuntos particulares, utilize o e-mail da professor.
III - AVALIAÇÕES
Na Sala de Aula, estarão disponíveis as duas Avaliações Parciais e a Avaliação Final, localizadas na caixa Avaliações; consulte o Cronograma da disciplina.
Relativamente a cada uma das Avaliações:
- Não esqueça de colocar seu nome, o nome da disciplina e o pólo no qual está inscrito.
- Há duas opções para apresentar suas soluções:
- Digitá-las utilizando programas que “aceitem” a simbologia matemática, como o Microsoft Word com Equation ou LaTeX;
- Digitalizar ("scanear") o manuscrito, que deve ser feito com letra legível. Tal digitalização deverá ser feita num ÚNICO ARQUIVO e em PDF. Cuidado, NÃO utilize o padrão IMAGEM.
- As avaliações deverão ser enviadas pela própria plataforma. Siga os seguintes passos:
- Clique na avaliação desejada;
- Abaixo da avaliação, clique em "ENVIAR ARQUIVO" para escolher o arquivo que contém suas soluções, previamente salvo em seu computador (ou CD ou "pendrive").
- Uma vez escolhido, clique em "ENVIAR ESTE ARQUIVO". Pronto, seu arquivo foi enviado!
Não é preciso enviar o enunciado das questões.
Não coloque apenas as respostas dos exercícios, pois só serão consideradas as que estiverem devidamente justificadas; escreva suas soluções de forma que qualquer outro professor possa ler e entender. A solução de um exercício é a transmissão por escrito de um raciocínio.
Caso estude com vários amigos (o que é extremamente válido) e tente resolver os exercícios em grupo, lembre-se de que a redação final dos exercícios é individual.
As Avaliações devem ser resolvidas e enviadas (pela plataforma) até a data determinada pelo o professor responsável, que as corrigirá na plataforma, com comentários sobre os possíveis erros. Verifique o que errou e refaça esses exercícios, observando os comentários feitos. Para acessar a correção clique na avaliação desejada a partir da data prevista em cronograma, ou alguns dias antes.
Tenha certeza, antes da data de envio das avaliações, que você sabe digitilazar seu manunscrito (se esta for sua escolha) , pois a plataforma NÃO aceita atrasos.
Conteúdo das Avaliações :
1ª Avaliação Parcial (1ªAP): Aulas 1, 2, 3.
Avaliação Final ( AF): Aulas 7,8,9 (acumulativo).
Datas de envio das Avaliações Parcias:
1ª Avaliação Parcial (1ªAP): até 27/09
2ª Avaliação Parcial (2ªAP): até 20/10
A entrega de pelo menos uma Avaliação Parcial (1ªAP ou 2ªAP) é obrigatória, isto é, quem não entregar uma delas, será desligado do curso.
No final do trimestre, será realizada a Avaliação Final (AF). Cada uma das Avaliações Parcias valerá 20 pontos e a Avaliação Final valerá 60 pontos. Você será aprovado se tiver alcançado média final maior ou igual a 60 pontos.
Data de envio da Avaliação Final (AF) : até 08/11
Quem não enviar a Avaliação Final (AF) obterá nota zero e estará automaticamente reprovado.
O pedido de revisão das Avaliações deverá ser feito por email. Para as datas, consulte o cronograma.
A Sala de Tutoria não deverá ser utilizada para esclarecimento sobre notas e correção de avaliações; por se tratarem de assuntos particulares, deverá ser utilizado o e-mail da professor.
IV – MATERIAL DIDÁTICO
O texto utilizado na disciplina Números Inteiros foi escrito pelo Professor André Luiz C. dos Santos e está assim estruturado:
Aula 1. Fundamentação dos Números Inteiros;
Aula 2. Indução Matemática;
Aula 3. Binômio de Newton;
Aula 4. Algoritmo da Divisão;
Aula 5. Divisibilidade;
Aula 6. Máximo Divisor Comum;
Aula 7. Algoritmo de Euclides;
Aula 8. Mínimo Múltiplo Comum;
Aula 9. Números Primos;
Os exercícios são parte importante do aprendizado. Ninguém aprende Matemática apenas com uma leitura dos exercícios propostos. Escreva suas soluções de forma que qualquer outro professor possa ler e entender. A solução de um exercício é a transmissão por escrito de um raciocínio. Em particular, neste curso, serão indicados alguns exercícios a cada seção. Isto não significa que os outros exercícios devam ser desprezados, ao contrário, são de extrema importância e são fortes candidatos a compor as avaliações. Portanto, na sala de tutoria, somente serão discutidos os exercícios indicados.
De maneira geral, o conteúdo das aulas é suficiente para entender os principais resultados desta disciplina, como também para resolver as Avaliações. Entretanto, é sempre enriquecedor buscar outras bibliografias. Procure resolver as questões utilizando os resultados dados no texto, citando-os adequadamente, justificando sempre suas respostas. Caso julgue necessário utilizar algum resultado fora do texto, enuncie-o, demonstre-o e cite a fonte bibliográfica.
Imprima este guia e consulte-o sempre que precisar de alguma informação.
Você Sabia?
Pierre de Fermat (1601-1665), jurista de profissão, foi um matemático que ficou conhecido em particular pelo seu trabalho na teoria dos números. O famoso "Último Teorema de Fermat" afirma que não há solução para a equação
xn+ yn = zn
se n for um inteiro maior do que 2 e x, y e z naturais (inteiros > 0).
No seu exemplar da "Aritmética" de Diofanto, Fermat escreve numa margem aquele enunciado e diz que tem uma demonstração, mas que ela não cabe namargem. Esta conjectura ficou por ser demonstrada e constituiu um verdadeiro desafio para os matemáticos ao longo dos tempos, apesar de parecer simples e oenunciado ser fácil de entender. Ao longo destes séculos, houve inúmeraspessoas que anunciaram terem demonstrado a conjectura, mas foram sendoencontrados erros, na maior parte dos casos bastante grosseiros.
Até que, em Junho de 1993, Andrew Wiles, matemático inglês da Universidade de Princeton (Estados Unidos), apresenta, no famoso seminário anual de matemática em Cambridge, o que considera ser a demonstração do último teorema de Fermat, resultado de um trabalho de 7 anos. Mas é descoberta uma falha nessa demonstração, que ocupava aproximadamente 200 páginas. Com a colaboração de Richard Lawrence Taylor, da Universidade de Cambridge (no Reino Unido), Wiles consegue corrigir o erro e em Outubro de 1994 apresenta essa correção. Fica assim concluída a demonstração do chamado último teorema de Fermat, cerca de 350 anos após ter sido enunciado. É curioso que este resultado, mesmoantes de provado, tenha sido sempre conhecido pela designação de último teorema de Fermat em vez de última conjectura de Fermat, como teriasido mais natural.
Um método rápido para o cálculo doquadrado de um número da forma a5 é o seguinte: basta multiplicar apor a + 1 e escrever o resultado seguido de 25. Por exemplo, paracalcular o quadrado de 25 fazemos 2 x 3 = 6 e escrevemos este resultado seguido de 25, isto é, 625. A justificativa é muito simples:
(a5)2= (10 a + 5)2 = 100 a 2 + 100 a + 25 = 100 a(a+1) + 25
Se chamamos de b o número a(a+1), então 100 b tem representação decimal b00, que quando somada a 25 tem-se b25. Na realidade, este método pode ser generalizado para um númeroda forma a1 a2 ... an-15, no entanto,sua praticidade não será garantida.
Quando um número N é divisível por 13? Uma regra simples para verificação da divisibilidade de um número N por 13 é a seguinte: quadruplique o último algarismo de N, e adicone este produto aonúmero formado por N sem o último algarismo. Por exemplo, se o número que você está testando é 345678, você adicionará 32 = 4 x 8 ao número 34567. Repita este processo até que se chegue a um número que você tenha certeza de que é divisível ou não por 13. O mesmo acontecerá ao número N ...
O que logarítmos tem a ver com terremotos? Muito ... Em 1935, Charles Richter definiu a magnitude M de um terremoto como sendo
onde I é a intensidade do terremoto, medida pela amplitude de um sismógrafo situado a 100 Km do epicentro do tremore S é a intensidade de um "terremoto padrão", cuja a amplitute é de1micron = 0,0001 cm.
A magnitude de um terremoto padrão é
Richter estudou vários terremotos que ocorreram entre 1900 e 1950. O maior teve magnitude de 8,9 em sua escala, e omenor teve magnitude 0. A escala foi inventada por Richter para que os números ligados a terremotos fossem mais manejáveis. Para se ter uma idéia melhor, cadaunidade na escala Richter indica um tremor dez vezes mais intenso. Por exemplo, um terremoto de magnitude 6 é dez vezes mais forte que um terremoto demagnitude 5; já um terremoto de magnitude 7 é 10 x 10 = 100 vezes mais forteque um de magnitude 5, enquanto um terremoto de magnitude 8 é 10 x 10 x 10 =1000 vezes mais forte que um de magnitude 5.
O número e foi estudado primeiramente pelo matemático suíço Leonhard Euler em 1720, embora suas existência fosse mais ou menos conhecida por John Napier, o inventor dos logarítmos, em 1614. Euler foi o primeiro a usar a letra e para denotar este número em 1727 (o fato de ser e a letra do seu primeiro sobrenome é uma coincidência). Às vezes, o número e é chamado de número de Euler ou contante de Napier. Um modo efetivo de se calcular o número e é usar a soma infinita:
e = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + ...
Euler provou que o número e um número irracional, de modo que ele não admite expansão decimal finita, nemmesmo periódica. Na verdade, o número e é um número trancedental, ou seja, não é raiz de polinômio algum com coeficientes racionais.
Que dia você nasceu? Aqui um truque para mostrar aum amigo, ou aos seus alunos. Fale para uma pessoa para pensar na data de nascimento dela e que você irá advinhar tal data.
Os passos são os que seguem:
Passo 1) Peça a pessoa que anote o número do mês de nascimento: Janeiro = 1,Fevereiro = 2, etc ...
Passo 2) Multiplique-o por 5;
Passo 3) Adicione 6;
Passo 4) Multiplique o total por 4;
Passo 5) Adicione 9;
Passo 6) Multiplique esse total, novamente, por 5;
Passo 7) Finalmente, peça a ele que adicione ao total obtido o dia em quenasceu. Por exemplo, se ele nasceu dia 18, adicione 18, etc ...
Agora pergunte pelo total obtido. Mentalmente, subtraia 165, e você irá ter o mês e o dia em que ele nasceu.
A justificativa do "truque" decorre diretamente da igualdade
5[4(5M + 6) + 9] + D =100 M + D + 165
onde M é o número do mês de nascimento e D o dia de nascimento.
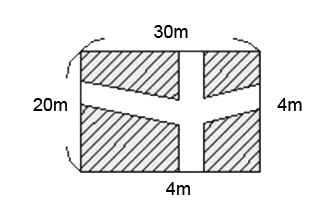
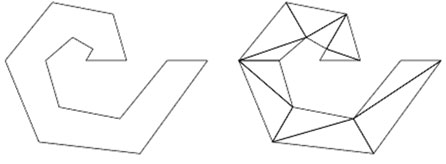
Triangularização é a divisão de umasuperfície ou de um polígono num conjunto de triângulos, normalmente com arestrição de que cada lado de um triângulo é inteiramente compartilhado pordois triângulos adjacentes. Foi provado em 1925 que toda superfície tem umatriangularização, mas isto pode requerer uma quantidade infinita de triângulos. Uma superfície com um número finito de triângulos em sua triangularização é chamada de compacta.
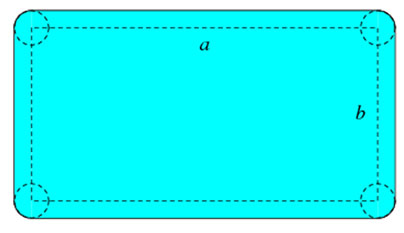
O "retângulo arredondado" é a forma geométrica acima que é obtida apartir de um retângulo de lados a e b e de quatro círculos comcentros nos vértices deste retângulo cujos raios são iguais a r. Ele temárea
e perímetro,
O conceito de infinito pode serutilizado para determinar o perímetro de um círculo. Com efeito, tal como fez Arquimedes, esse valor pode ser calculado a partir da sucessão dos perímetrosdos polígonos regulares inscritos. À medida que o número de lados aumenta, operímetro do polígono aproxima-se cada vez mais do perímetro do círculo. Assim, o perímetro do círculo corresponde ao limite da sucessão dos perímetros dospolígonos inscritos, quando o número de lados tende para infinito.
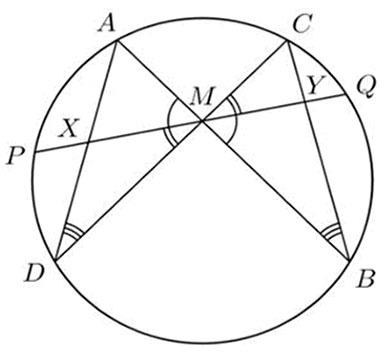
A figura acima ilustra um famosoresultado da geometria plana, conhecido por "Teorema da Borboleta" que afirma o seguinte: Seja M o ponto médio de uma corda PQ de uma circunferência, através da qual outras duas cordas AD e BC são desenhadas. AD corta PQ no ponto X e BC corta PQ no ponto Y. Então M é o ponto médio de XY. A figura já explica o porquê do nome do teorema ...
Num grupo de 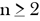 pessoas sempre há pelo duas pessoas que conhecem o mesmo número de pessoas.
pessoas sempre há pelo duas pessoas que conhecem o mesmo número de pessoas.
Em 1742, numa carta a Leonhard Euler(1707-1783), o matemático Christian Goldbach (1690-1764) formulou aseguinte conjectura: "Todo o número ímpar superior ou igual a 7 ésoma de três números primos". Em resposta, Leonhard Euler observou que essa conjectura é consequência da seguinte: "Todo o número par superior ou igual a 6 é soma de dois números primos". Esta última conjectura é conhecida como conjectura de Goldbach. Até hoje ainda não se sabe se é verdadeira. Para todos os números pares para os quais foram feitos cálculos até hoje, sempre se encontraram dois números primos que asatisfazem. E muitos matemáticos tentaram efetuar cálculos:
- Georg Cantor (1845-1918), efetuou em 1894 todas as decomposições possíveis, como soma de dois números primos, de todos os números pares inferiores a 1000.
- Aubry estendeu a lista de Cantor até 2000.
- R. Haussner em 1897 estendeu essa tabela até 5000. Em 1937 o matemático soviético I.M. Vinogradov demonstrou, usando somas trigonométricas adequadas, que qualquer número ímpar suficientemente grande é soma de três números primos.
O número máximo de regiões que nretas dividem um circulo é dado por 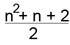 .
.
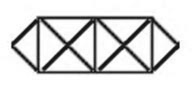
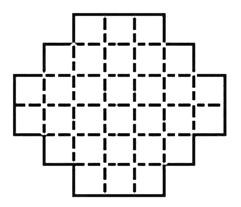
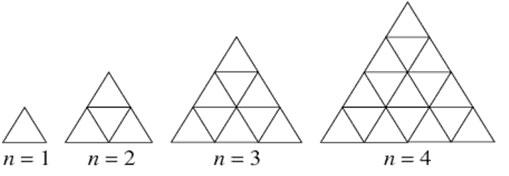
O número total de triângulos, incluindo os invertidos, nas figuras acima é dado 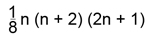 se
se 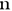 é par e
é par e  se n é ímpar.
se n é ímpar.
Os primeiros valores são 1, 5, 13, 27,48, 78, 118, 170, 235, 315, 411, 525, 658, 812, 988, 1188, 1413, 1665.
O "salinon" é a figura ilustrada acima formada por quatro semi-círculos conectados. A palavra salinon vem do grego e a figura tem este nome por lembrar um saleiro. Se o raio do maior semicírculo é R e raio do menor semicírculo (central) é r, então o raio dos dois semicírculos menores é (R - r)/2.
No"Livro dos Lemas", Arquimedes provou que o salinon tem área igual ao do círculo (em vermelho) cujo o diâmetro é o segmento que une os pontos inferior e superior dos semi círculos menor e maior, repectivamente, a saber, 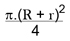 .
.
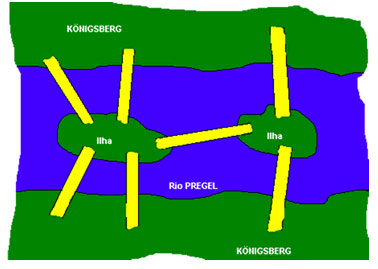
Conta-se que, noséculo XVIII, havia sete pontes cruzando o rio Pregel, que banhava a pequenacidade universitária prussiana de Königsberg, hoje Kaliningrad, Rússia. Quatro delas ligavam as margens opostas a uma pequena ilha formada nesse rio, outras duas ligavam as margens opostas a uma outra ilha, próxima à primeira, e aúltima ponte ligava as duas ilhas, conforme a figura. Os habitantes deKönigsberg costumavam passear na sua cidade nas tardes ensolaradas de Domingo, mas nunca tinham conseguido dar um passeio especial:
sair de casa, atravessar todas as pontes uma só vez e regressar a casa. No entanto a dúvida quanto à possibilidade persistia. Euler, em 1735, conseguiu provar, com clareza, que não era possível dar o tal passeio. Este episódio deu origem agrandes teorias matemáticas muito exploradas nos dias atuais.
Os matemáticos gregos estudaram três problemas de Geometria que desempenharam papel importante no desenvolvimento da Matemática. Eles são problemas deconstrução e resistiram a todas as tentativas dos gregos para resolvê-los utilizando somente a régua sem graduação e o compasso, os únicos instrumentos utilizados por Euclides nos Elementos. Os três problemas,
que ficaram conhecidos como os três problemas clássicos, são : 1) Aduplicação do cubo, 2) A quadratura do círculo e 3) A trissecção do ângulo. Desde o século XIX é sabido que estes problemas não podem ser resolvidos somente com a régua e o compasso ...
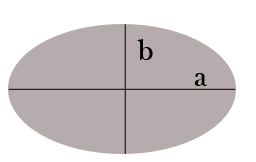
A área de elipse de semi-eixos ae b é dada por 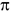 a b e seu perímetro por (a + b)
a b e seu perímetro por (a + b) 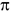 .
.
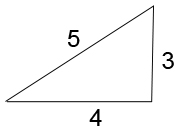
A mais bela e simples prova do Teoremade Pitágoras ...
Se dois números de dois algarismos possuem algarismos das dezenas iguais e seus algarismos das unidades têm soma 10, pode-se calcular seu produto facilmente, multiplicando-se o algarismo da dezena pelo seu consecutivo e acrescentando-se a direita deste resultado, o produto dos algarismos das unidades. Por exemplo : 77 x 73 multiplica-se 7 x 8= 56 e 7 x 3 = 21, assim 77 x 73 = 5621.
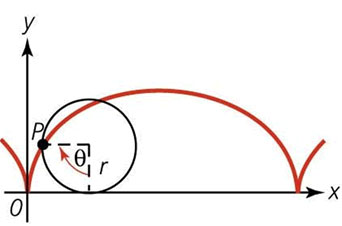
Foi Galileu Galilei (1564-1642) quem descobriu por volta de 1600 a curva hoje chamada ciclóide, traçada por um ponto sobre o bordo de uma roda quando esta rola num caminho horizontal.
Galileu tentando achar a sua área recortou um molde em papel e concluiu que a área era aproximadamente igual a três vezes a área do círculo gerador. Em 1637, Roberval (1602-1675) publica umtrabalho com o cálculo exato da área sob um arco de ciclóide.
Galileu recomendou seu estudo a seus amigos, incluindo Mari Mersenne (1588-1648). Mersenne informou René Descartes(1506-1650) e outros matemáticos da época.
Em 1638, Descartes desafia seus contemporâneos a determinar a tangente em um ponto qualquer da ciclóide. Pierre de Fermat (1601-1665) aceitou o desafio e resolveu o problema sem muita dificuldade: seu método, mais amplo, atingiu diretamente o objetivo, mesmo nesse caso, em que se tratava de uma curva "mecânica" ou "transcendente" como hoje diríamos. Em 1644, o discípulo de Galileu, Evangelista Torricelli (1608-1647) inventor do barômetro publicou sua descoberta da área sob o arco deciclóide.
Em junho de 1658 , Blaise Pascal (1632-1662) em um famoso desafio aos matemáticos da época, propunha determinaro comprimento de um arco da ciclóide, seu centro de gravidade e a superfície dosólido de revolução formado pela rotação de um arco de ciclóide em torno do eixo x ou y. Como prêmio foram depositados 60 dobrões (moeda de ouro espanhola), e as soluções deveriam ser entregues até 1º de outubro de1658. O desafio suscitou enorme interesse, dando origem a volumosacorrespondência. Apenas duas soluções deram entrada, nenhuma perfeita mente exata; quem mais se aproximou foi o inglês John Wallis (1616-1703).
Quando Wallis mandou sua resposta aodesafio de Pascal, Christopher Wren (1632-1723) enviou a Pascal sua retificaçãoda ciclóide, encerrando a curva entre dois setores poligonais em de forma dedentes de serra. A determinação do comprimento desta curva fôra por muitos declarada impossível, inclusive por Descartes.
No decorrer destas investigações originou-se alguns conflitos de prioridade: os franceses procuravam negar a Torricelli todo e qualquer mérito, chegando até acusá-lo de plágio de Roberval, e infelizmente o próprio Pascal tomou parte muito ativa e pouco recomendável nesta controvérsia.
Em 2005, o número π foi calculado comuma aproximação de 1,24 trilhões de casas decimais pelo Professor Yasumasa Kanada e sua equipe de pesquisadores. Eles simplesmente bateram o recorde mundial! O recorde anterior, do próprio Kanada, obtido em 1999 era de 206.158 bilhões de casas decimais...
Escolha qualquer número inteiro maior que zero. Se ele é par exiba sua metade e se ele for ímpar exiba seu triplo mais uma unidade. Repita este processo seguidas vezes. Você concluirá que o resultado é sempre igual a 1.
Em que dia da semana você nasceu? Apesar de você estar lá no momento de seu nascimento, você não pode lembrar exatamente o dia da semana que era. O métodoa seguir vai ajudá-lo a descobrir isso! Aqui está um pequeno truque para ajudaro dia da semana que era:
Passo 1) Escreva os dois últimos dígitos do ano em que nasceu. Chame-o de A.
Passo 2) Divida esse número, isto é, divida A por quatro. Chame-o quociente da divisão de B ( caso haja resto na divisão, depreze-o)
Passo 3) Na tabela abaixo, encontre o número correspondente seu ao mês de nascimento. Chame-o de C.
Passo 4) Chame de D o dia do seu nascimento (por exemplo, se você nasceu no dia 12, faça D=12.
Passo 5) Agora adicione A + B + C + D. Divida esta soma por 7. O resto você recebe éa chave para o dia da semana.
Passo 6) Na tabela de dias a seguir, de acordo com o resto da divisão correspondeobtido no "passo 5" , você determina o dia da semana em que você nasceu!
Tabela de meses |
Janeiro = 1 (0-bissexto) |
Julho = 0 |
Fevereiro = 4 (3-bissexto) |
Agosto = 3 |
Março = 4 |
Setembro = 6 |
Abril = 0 |
Outubro = 1 |
Maio = 2 |
Novembro = 4 |
Junho = 5 |
Dezembro = 6 |
Tabela de dias |
|
Domingo = 1
|
|
Segunda = 2
|
|
Terça = 3
|
|
Quarta = 4
|
|
Quinta = 5
|
|
Sexta = 6
|
|
Sábado = 0
|
Você sabia que 153 = 13 + 53 + 33?

Johnvon Neumann (1903 - 1957) nasceu em Budapeste, na Hungria. Aos 6 anos, era capaz de resolver mentalmente problemas de divisãocomo por exemplo 78.463.215 por 49.673.235.
Por volta dos 8 anos, obteve seu diploma de Cálculo na faculdade e como brincadeira podia memorizar, apenas olhando, os nomes, endereços e números de telefone de uma coluna em uma lista telefônica. Com apenas 23 anos de idade, escreveu um livro chamado Os Fundamentos Matemáticos da Mecânica Quântica, utilizado no desenvolvimento da energia atômica.
Von Neumann foi um dos matemáticos mais notáveis de nossos tempos. Como tantosoutros matemáticos, ele prestou contribuições importantes tanto à Ciênciaquanto à Matemática. Von Neumann se sentia particularmente fascinado pelosjogos de estratégia e de acaso. Assim, não é de se surpreender que ele foi oinventor de um ramo da Matemática chamada Teoria do Jogos.
Empregando as probabilidades envolvidas em jogos do acaso e trabalhando com estratégias que produzem "vencedores" em jogos de tomar decisões, a teoria dos jogos de von Neumann pode solucionar problemas de economia, de Ciência e de Estratégia Militar.
Em 1930, von Neumann foi para os Estados Unidos assumir o cargo de professor de Física Matemática na Universidade de Princeton. Tornou-se interessado no uso decomputadores de grande escala e construiu um dos primeiros cérebros eletrônicos modernos, chamado MANIAC (Mathematical Analyzer, Numerical Integrator and Computer). Como conselheiro do governo americano durante a 2ª Guerra Mundial, exerceu influência no projeto de armas e mísseis nucleares.
Von Neumann tinha muitos interesses intelectuais, mas seu maior divertimento era resolver problemas. Algumas vezes, enquanto viajava, ele se envolvia de tal forma com um problema que tinha que telefonar à sua esposa para descobrir porque havia feito aquela viagem. É devido à habilidade de John von Neumann de resolver problemas que nossos horizontes matemáticos se ampliaram.
![]() .
.

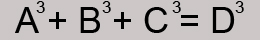

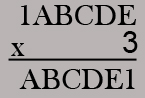

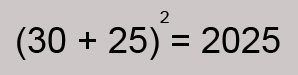
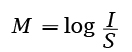
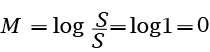
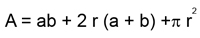

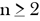 pessoas sempre há pelo duas pessoas que conhecem o mesmo número de pessoas.
pessoas sempre há pelo duas pessoas que conhecem o mesmo número de pessoas. 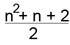 .
. 
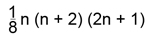 se
se  é par e
é par e  se n é ímpar.
se n é ímpar. 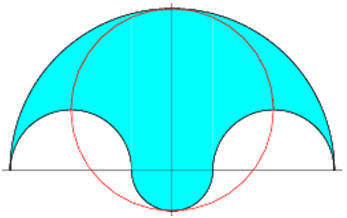
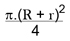 .
.  Conta-se que, noséculo XVIII, havia sete pontes cruzando o rio Pregel, que banhava a pequenacidade universitária prussiana de Königsberg, hoje Kaliningrad, Rússia. Quatro delas ligavam as margens opostas a uma pequena ilha formada nesse rio, outras duas ligavam as margens opostas a uma outra ilha, próxima à primeira, e aúltima ponte ligava as duas ilhas, conforme a figura. Os habitantes deKönigsberg costumavam passear na sua cidade nas tardes ensolaradas de Domingo, mas nunca tinham conseguido dar um passeio especial: sair de casa, atravessar todas as pontes uma só vez e regressar a casa. No entanto a dúvida quanto à possibilidade persistia. Euler, em 1735, conseguiu provar, com clareza, que não era possível dar o tal passeio. Este episódio deu origem agrandes teorias matemáticas muito exploradas nos dias atuais.
Conta-se que, noséculo XVIII, havia sete pontes cruzando o rio Pregel, que banhava a pequenacidade universitária prussiana de Königsberg, hoje Kaliningrad, Rússia. Quatro delas ligavam as margens opostas a uma pequena ilha formada nesse rio, outras duas ligavam as margens opostas a uma outra ilha, próxima à primeira, e aúltima ponte ligava as duas ilhas, conforme a figura. Os habitantes deKönigsberg costumavam passear na sua cidade nas tardes ensolaradas de Domingo, mas nunca tinham conseguido dar um passeio especial: sair de casa, atravessar todas as pontes uma só vez e regressar a casa. No entanto a dúvida quanto à possibilidade persistia. Euler, em 1735, conseguiu provar, com clareza, que não era possível dar o tal passeio. Este episódio deu origem agrandes teorias matemáticas muito exploradas nos dias atuais.
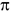 a b e seu perímetro por (a + b)
a b e seu perímetro por (a + b)